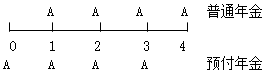
(1)预付年金(即付年金、期初年金):从第一期起,各期期初收付的年金

①n期内共发生n笔年金(n个A);
②第1笔年金发生在时点0(第一期期初),最后1笔年金发生在时点n-1(最后一期期初)。
【提示】
在期数相同的情况下,普通年金与预付年金的年金个数相同(n期内有n笔年金);二者的区别仅在于收付款时间的不同:普通年金发生于各期期末(1~n),在0时点(第一期期初)没有发生额;预付年金发生于各期期初(0~n-1),在n时点(最后一期期末)没有发生额。
(2)预付年金终值:由于预付年金的每一笔年金都比普通年金提前一期发生,因而在计算终值时,预付年金的每一笔年金都要比普通年金多一个计息期。

预付年金终值=普通年金终值×(1+i)

=A×[(F/A,i,n+1)-1]
即:预付年金终值系数是在普通年金终值系数基础上,期数加1,系数减1的结果。
【示例】
某公司打算购买一台设备,付款方式为每年初支付200万元,3年付讫。假设年利率为5%,复利计息。则该公司购置设备的付款额终值为:
F=200×(F/A,5%,3)×(1+5%)=200×[(F/A,5%,4)-1]=662.02(万元)
(3)预付年金现值:由于预付年金的每一笔年金都比普通年金提前一期发生,因而在计算现值时,预付年金的每一笔年金都要比普通年金少折现一期。

预付年金现值=普通年金现值×(1+i)
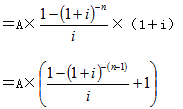
=A×[(P/A,i,n-1)+1 ]
即:预付年金现值系数是在普通年金现值系数基础上,期数减1,系数加1的结果。
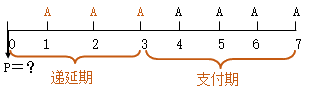
(1)递延年金(延期年金):不是从第一期开始,而是若干期后才开始发生的每期期末等额收付款项。

递延期=第一笔年金发生的期末数-1
支付期=年金A的个数
(2)递延年金现值的计算
①分段折现法
在递延期末或支付期初(第一笔年金发生的前一个时点)将时间轴分成两段。
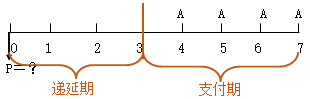
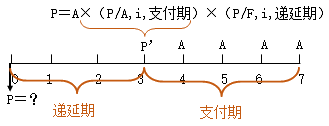
先计算支付期的普通年金现值(P′),即支付期内各期年金在支付期初或递延期末(第一笔年金发生的前一个时点)的现值合计,再计算P′在递延期初的复利现值。
②插补法
假设递延期内也有年金发生,先计算“递延期+支付期”的年金现值,再扣除递延期内实际并未发生的年金现值。
P=A×[(P/A,i,递延期+支付期)-(P/A,i,递延期)]
(1)永续年金(永久年金):无限期收付款项的年金

【提示】永续年金没有到期日,因而没有终值。
(2)永续年金现值=A/i
【示例】
某种永续年金每年收款1200元,折现率为10%,则该永续年金的现值可近似地计算为:P=1200/10%=12000(元)
以上就是关于2021年初级审计师考试考点:预付、递延、永续年金的介绍,更多备考资料,可以关注唯学网。